Dr. Carlos M. Martínez M.
cmmm7031@cmmm7031
Prof. Titular jubilado de la Universidad de Carabobo
República Bolivariana de Venezuela
Trazado de rectas en el espacio E4D. ©
20 de Febrero 2022
1. Introducción
La geometría euclidiana es una rama de la matemática que se encarga del estudio de los espacios que cumplen con los axiomas o postulados de Euclides (No es objetivo en este blog discutir la imposibilidad o la posibilidad de la existencia de una cuarta dimensión espacial, en nuestro mundo real y por ahora, este punto lo dejaré a un lado y dedicaré este blog a la traza de líneas rectas en el espacio 4D. Escritos, puntos de vistas y comentarios a favor o en contra de la existencia o no existencia de la cuarta dimensión existen muchísimos, destacan por mencionar algunos los trabajos de los siguientes autores: Ludwig Schläfli con su «Über die Hypothesen welche der Geometrie zu Grunde liegen» de 1854, Frederick Riemann en 1854 fundó el campo de la geometría de Riemann y estudio de variedades en el espacio n-dimensional, diferenciales y con las métricas que llevan su nombre. Alice Boole, entre 1880 y 1890 halló que los politopos regulares en 4D, son seis. Charles Howard Hinton con su artículo de 1880, titulado: «What is the Fourth Dimension?», también hizo otros aportes importantes, se le conoce por acuñar la palabra teseracto (en inglés: tesseract) para su sistema de visualización de geometría en 4D, fue autor de la novela de ciencia ficción titulada «Romances científicos«. Albert Einstein con su teoría de la relatividad de 1905-1915 definió el espacio de la cuarta dimensión como una entidad única que llamó: «Espacio-tiempo», unificando tres dimensiones espaciales con una cuarta dimensión temporal. En 1921 (aunque sus ideas se remontan a 1919), Theodor Kaluza publicó, una teoría que es una generalización de las ecuaciones del campo de Einstein. Planteadas en principio, en el espacio-tiempo de Einstein y una quinta dimensión adicional. En 1926, Oskar Klein tomó las ideas de Kaluza y las combinó con algunas ideas teóricas de la mecánica cuántica, cuantificó el valor de la carga en el modelo y la pequeñez e inobservabilidad práctica de la dimensión adicional. La teoría teoría de Kaluza-Klein trató de unificar la teoría de la gravedad de Einstein y el electromagnetismo de Maxwell, usando un modelo geométrico en un Espacio-tiempo 5D. Esta teoría se conoce como la teoría de Kaluza-Klein[5] y es una generalización de la teoría de la relatividad general de Einstein. Florian Cajori con su trabajo «Origins of Fourth Dimension Concepts» de 1926, publicado por Taylor & Francis, recopila las impresiones y opiniones de muchos matemáticos de renombre acerca de la existencia de la 4D, en su escrito hace un recorrido desde la época de Platón, pasando por Henry Moore, hasta Hernann Minkosky y años posteriores. La idea de un mundo espacial tridimensional y uno temporal quedó arraigada en nuestras mentes como una verdad o una realidad inalterable. Decimos, «Todo lo que está a nuestros alrededores, está enmarcado y se define con tres dimensiones espaciales: anchura, profundidad y altura y una temporal». La frase: «Nuestro espacio físico es tridimensional» es recurrente. Es común, escuchar esa frase repetidamente a todo nivel, es la percepción que tenemos de nuestra realidad. En este blog, sólo me centraré y dedicaré mi esfuerzo a trazar gráficas de lugares geométricos en un espacio matemáticamente posible (el espacio E4D) y de la posibilidad de lograrlo «a las pruebas me remito». La técnica de la traza de lugares geométricos en un espacio 4D es una tarea que hasta el surgimiento de esta idea, mi experiencia me indica, que todavía muchos creen imposible, otros son más flexibles y ha aceptado la idea, pero con cierto recelo. Los autores primarios de la teoría 4D, son autores que me anteceden y son referencias de este trabajo. Muchos de ellos, estuvieron a un paso de lograrlo y sus intentos son muy válidos, otros utilizaron otras técnicas de visualización de la 4D, como: el métodos de las sombras, curvas de niveles, proyecciones espectroscópicas, métodos de colores y otras, en mi caso logré concretar algo más sólido: Trazar gráficas en 4D tal y como tradicionalmente lo hemos hecho en dos y tres dimensiones y con procedimientos similares a los conocidos con algunas y ligeras modificaciones. La aplicación inmediata de la idea, a la que catalogo como novedosa, poderosa, interesante y revolucionaria, es su aplicación directa en la traza de lugares geométricos en el espacio de cuatro dimensiones, espacio que se decidió llamar: «Espacio Euclidiano 4D» o simplemente «Espacio E4D» [1]. Para mi, ha sido de gran satisfacción haber alcanzado y desarrollo esta idea, la traza lugares geométricos en un espacio superior a tres dimensiones, aunque confieso que su llegada, vino acompañada de algunas emociones encontradas, en éstos tiempos de convulsiones en mi país de origen y en el mundo, caben mencionar: la pésima situación que viven nuestras universidades venezolanas por varios motivo y la permanencia en el tiempo de esta terrible pandemia (el COVID-19). La divulgación del trabajo y las expectativas esperadas para su presentación han sido afectadas por ambos. La pandemia mundial generalizada es la principal causa, su permanencia en el tiempo ha hecho mucho daño: ha causado horrorosos y difíciles momentos en nuestras familias y ha afectado negativamente el desarrollo de nuestros trabajos.
Retomando nuestro objetivo: El basamento matemático de la metodología es muy sólido; por ahora no se hará público, por lo menos hasta que concrete una discusión más formal en medios y en espacios destinados; para ello (sin menospreciar este medio), como: congresos, simposios o publicaciones en revistas científicas adecuadas y pertinentes. La idea de la traza lugares geométricos en dimensión superiores intuyo es altamente deseada y demanda aún cuando no ha sido pedido explícitamente. La estadística es de las ramas de la ciencia que dispone de herramientas avanzadas para el estudio de fenómenos en alta dimensión: cabe mencionar: componentes principales, biplot, entre otras. Se trata de representar fenómenos de la alta dimensión en baja dimensión (2D o 3D); pero, en el proceso hay pérdida de información. La herramienta que en este blog se presenta será una herramienta de apoyo para el avance y el estudio de fenómenos en alta dimensión específicamente en 4D, me atrevería a decir, que mucho campos de la ciencia se verán afectados de manera positiva. La teoría está enmarcada en la matemática, en las ramas de la Geometría y el Álgebra, con apoyo y basamento primario en la traza de lugares geométricos de baja dimensión. El trabajo del filósofo, matemático y físico francés padre de la geometría analítica René Descartes (1596-1650) a finales del siglo XVII, La Géométrie[4] y los sistemas de coordenadas cartesianas que llevan su nombre son uno de los pilares de apoyo de este trabajo. La técnica de trazar gráfica en el espacio E4D la inicié en año 2014 y en el año 2016 se publicó el primer ensayo: Geometría E4D[1], la técnica se ha venido perfeccionando en la medida que se ha adquirido mayores experiencias, la mejora de los algoritmos en la automatización y optimización en la traza de las variedades geométricas 4D es una de las metas. Dentro de las expectativas está la aceptación de la teoría y la validez de la metodología. Es de esperarse que un futuro cercano esta idea tendrá muchas aplicaciones e incidencias, se tendrán arduos debates del tema que tocarán de alguna manera, los cimientos y el enfoque de la teoría relativista y otras en la que subyacen los modelos físicos aceptados en estos tiempos. El objetivo de este blog es ilustrar la traza de lugares geométricos propios del espacio 4D; nos ocupa, específicamente y como objetivo inmediato: la traza de líneas rectas en el espacio E4D.
2. Marco teórico
Definición del problema: Supóngase que se da una ecuación en función de cuatro variables, dígase: x, y, z y w definida como la que describe en la ecuación 2.2. Se pide construir el lugar geométrico asociado a la ecuación dada en R4 (trace la gráfica en 4D).
f(x, y, z, w) = 0, (ec. 2.2)
Instrucciones para el trazado de variedades en el espacio E4D: En general, existen una cantidad infinita de puntos, P=(x, y, z, w) que satisfacen la ecuación 2.2. Aunque, se puede dar el caso donde ningún punto del campo de los números reales, cumpla con la condición de la ecuación 2.2. Es decir, no existe puntos reales que satisfagan dicha ecuación. En ese caso, el lugar geométrico es vacío en el campo de los números reales (ℛ) en 4D[2]. Sin embargo, nosotros vamos a trabajar con lugares geométricos no vacíos. Donde, cada punto P considerado, contiene cuatro coordenadas de ℛ que pertenecen al lugar geométrico. Para trazar los lugares geométricos en 4D, utilizaremos «en general» el método parametrizado clásico o el método clásico; donde, simultáneamente tres de las cuatro variables toman valores reales independientes entre sí y con una cuarta coordenada dependiente de al menos una de las tres primeras. Una infinidad de puntos que cumplan con la condición o ecuación permite la traza del lugar geométrico. Si se da el caso, que la cuarta coordenada pueda ser expresada únicamente y explícitamente en función de las tres primeras coordenadas, diríamos que la ecuación esta descrita en su forma explícita. Si no es el caso, porque la cuarta coordenada no puede ser despejada, como es el caso de ecuaciones no lineales más complejas, habría que calcular la cuarta coordenada por algoritmos numéricos iterativos o procedimientos matemáticos especiales, como por ejemplo: el algoritmo de bisección, el método de Newton u otros. Una vez determinados una cantidad de puntos «suficientes» para graficar, el siguiente paso es localizar y trazar los puntos en el sistema de referencia o sistema de coordenadas. Recomendable el uso de una mezcla de colores convenientemente para poder distinguir o diferenciar las diferentes capas o superficies del lugar que compone la variedad o el cuerpo geométrico que desea trazar. Para herramientas automatizadas use la paleta de colores RGB o similar. Para trazar líneas rectas en el espacio E4D, un sólo color de contraste con el fondo es suficiente. Definir la densidad de puntos y los colores también es importante y algunos casos tendrá que redefinir esos parámetros. Revise, si la escala del sistema de coordenadas 4D es adecuada y conveniente para la traza dicho lugar geométrico. Luego del trazado de puntos, identifique el lugar geométrico. Si es imposible identificar la variedad en los primeros intentos, modifique parámetros de forma y escalas de las variables involucradas, trace y trate de identificar nuevamente el lugar geométrico. En algunas ocasiones, tendrá que repetir esta tarea varias veces, sea creativo.
3. Rectas en el espacio E4D
Rectas en el espacio E4D: En el punto anterior a este párrafo, se consideró un método general para construir o trazar figuras geométricas en cuatro dimensiones. Las instrucciones del método fueron dadas de manera general, asumiendo que el lector dispone o no de una herramienta computarizada para trazar las gráficas de los lugares geométricos deseados en el espacio E4D. Continuando con la intención de aprender a utilizar el espacio 4D, en esta sesión seguiremos con el trazado de líneas rectas en 4D y en todos sus subespacios. La linea recta es uno de los lugares geométricos más sencillo de trazar en 4D (exceptuando el punto, el segmento y los vectores 4D, las instrucciones para la graficación puntos en 4D, ya fueron discutidos y publicados en sesiones anteriores a este blog). El trazado de rectas en el espacio 4D es bastante sencillo, no es necesario el uso de una herramienta computarizada para lograr el objetivo, con el uso de escuadras y reglas se puede hacer la tarea. Para figuras más complejas, como esferas, elipsoides 4D, la herramienta computarizada si es vital. Tengo la satisfacción de haber logrado diseñar un algoritmo computacional en lenguaje R para trazar dichas gráficas (El programa todavía no es público, su disponibilidad estará a disposición prontamente, sea paciente).
Definición paramétrica de la linea recta en 4D: Sea, P=(x, y, z, w) y P0=(x0, y0, z0, w0) puntos que pertenecen a un lugar geométrico L, en R4. Si, t es cualquier parámetro perteneciente a los números reales y las ecuaciones (3.1, 3.2, 3.3 y 3.4) que se muestran a continuación están referidas al lugar geométrico L, dicho lugar geométrico será una linea recta paralela al vector V=(a, b, c, d) en R4 . Las ecuaciones dadas son las ecuaciones paramétricas que definen a la linea recta en R4.
x = x0 + t * a, (ec. 3.1)
y = y0 + t * b, (ec. 3.2)
z = z0 + t * c, (ec. 3.3)
w = w0 + t * d, (ec. 3.4)
Si, ninguno de los números o componentes del vector V es cero, dígase: a, b, c o d, se puede eliminar el parámetro t de las ecuaciones anteriores, para obtener:
(x – x0 )/a = (y – y0 )/b , (ec. 3.5)
(y – y0 )/b = (z – z0 )/c, (ec. 3.6)
(z – z0 )/c = (w – w0 )/d, (ec. 3.7)
que representan las ecuaciones simétricas de la línea recta en R4. El vector V define la dirección de la recta en R4 y los números: a, b, c y d, serán sus números directores o parámetros directores.
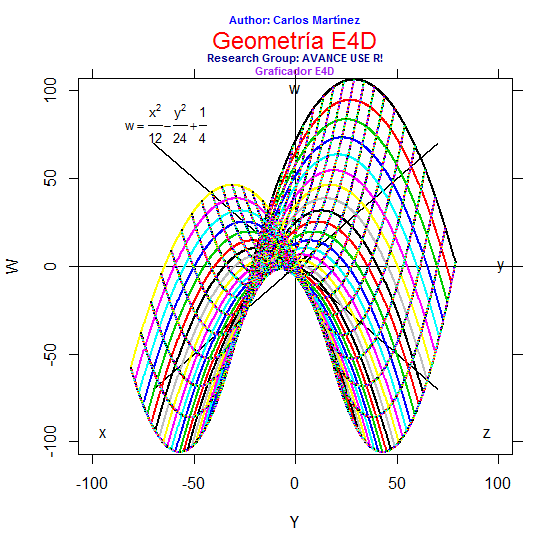
Ejemplo ilustrativo 3.1: Dada las ecuaciones (3.8, 3.9, 3.10 y 3.11) de un lugar geométrico en R4. Trace su lugar geométrico.
x = 10 + t * cos(pi/6), (ec. 3.8)
y = 15 + t * cos(pi/3), (ec. 3.9)
z = 10 + t * cos(pi/4), (ec. 3.10)
w = 25 + t * cos(pi/3), (ec. 3.11)
Solución: Se observa que las ecuaciones dadas, desde la 3.8 hasta la 3.10, definen el lugar geométrico . Se pude señalar que el lugar geométrico está parametrizado en función de del parámetro t. Las ecuaciones tienen las mismas estructuras de las ecuaciones que definen una linea recta en R4; por lo tanto, el lugar geométrico asociado a las ecuaciones dadas es una línea recta. También, se puede deducir que la línea recta L, pasa por el punto P=(10,15,10,25) y es paralela al vector director V, cuyas componentes son los números directores de la recta L. Así, V=(cos(pi/6),cos(pi/3), cos(pi/4), cos(pi/3)) cuyas compnentes representan los cosenos directores de la linea recta en R4.
A continuación, muestro los pasos generales para trazar la gráfica de la linea recta L en 4D, del ejemplo 3.1.
1) Escoja el sistema de coordenadas (x, y, z, w) con una escala conveniente que le permita trazar la recta en estudio, algo similar a la figura 3.1. El sentido de cada eje queda a su elección. En nuestro ejemplo, decidí escoger la distribución «PG» (Pata de Gallina), distribución tipo tripoide o tetraédrica para ubicar los ejes de coordenadas en R4.

Figura 3.1 Sistema de coordenadas 4D con una escala definida. (Fuente propia).
2) Determine el vector director de la recta con los números directores de las ecuaciones de la recta L. En nuestro ejemplo, el vector V=(cos(pi/6),cos(pi/3), cos(pi/4), cos(pi/3)) con punto de partida en el origen del sistema de coordenadas definido en el punto 1).
3) Trace el vector director (vector V ) de la recta L o uno proporcional a éste, que se adecue a la escala de su sistema de coordenadas definido en el paso 1); tal y como, se muestra en la figura 3.2. Conocido el vector V, ya Ud. conoce la dirección en R4 de la recta para su trazado. Como ya dispone de la dirección sólo faltaría la ubicación de la recta en su sistema de coordenadas 4D.
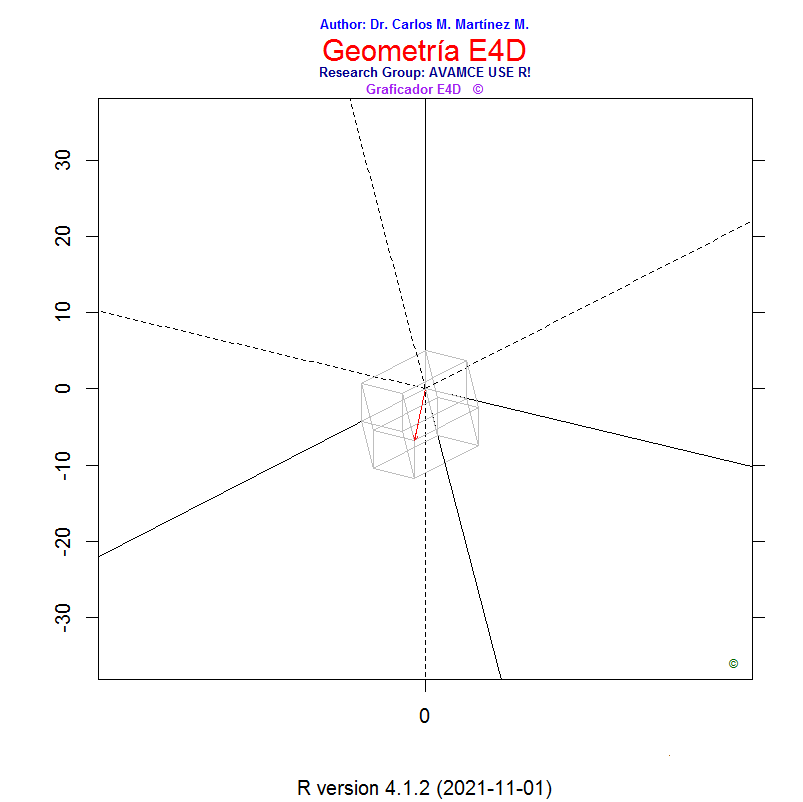

Figura 3.2 Trazado del vector director V de la recta L del problema 3.1 (Fuente propia).
4) Determine al menos un punto en R4 por donde pase la recta L. Utilice las ecuaciones dadas en el problema 3.1. En nuestro caso, calculamos tres puntos que pertenecen a la recta, P1, P y P2. Para ello, utilizamos los siguientes valores de t: -12*pi, 0 y +12*pi. Así: P1 = (-22,64, -3.84, -16.65, 6.15), P=(10, 15, 10, 25) y P2 = (42.68, 33.84, 36.65, 43.84).
5) Localice los puntos P1, P y P2 de la recta L en el sistema de coordenadas escogido en el paso 1). Utilice procedimiento de localización de puntos en 4D descrito en sesiones anteriores a este blog. En nuestro ejemplo se obtendrá algo similar a la figura 3.3.




Figura 3.3 Localización de los puntos P1, P y P2 de la recta L del problema 3.1. (Fuente propia).
6) Trace la recta L que pase por los punto P1, P y P2. En nuestro ejemplo, obtendrá una figura similar a la figura 3.4. Observe que la recta L del problema 3.1 es paralela a sus vector director V.


Figura 3.4 Trazado de la recta L, del problema 3.1. (Fuente propia).
¡Felicitaciones!, Usted logró trazar su primer lugar geométrico en R4. Con ambos «blogs», titulados: Localización de un punto en 4D y el trazado de rectas en el espacio E4D, Usted ya está preparado para trazar segmentos, vectores, rectas y curvas en 4D. Avance de este tópico en próximas sesiones.
Notas del autor: Es bienvenida la retroalimentación de los lectores. Para disfrutar de la belleza de un diamante hay que cortarlo, tallarlo y pulirlo, eliminando en el proceso impurezas e imperfecciones. Prepara tu mente que se avecinan nuevos retos. Si desea apoyar este proyecto contacte a su autor, le estaremos eternamente agradecido.
4. Bibliografía
- Martínez M. Carlos M. (2016). Geometría E4D. 1ra edición, ISBN: 978-980-12-8563-2. DOI: 10.13140/RG.2.1.2103.2720, ASIN: B01C1LRGT8.
- Lehmann, C. H., & Sors, M. S. (1953). Geometría analítica. Unión Tipográfica. Editorial: Hispano Americana.
- Leithold, L., (1998). El cálculo. Oxford University Press.
- Descartes, R., La Géométrie (éd. 1637) Discours de la méthode plus La Dioptrique, plus Les Météores, Jan Maire, 1637.
- Teoría de Kluza-Klein. (30 de Agosto de 2021) , en Wikipedia. https://es.wikipedia.org/w/index.php?title=Teor%C3%ADa_de_Kaluza-Klein&oldid=138001720





































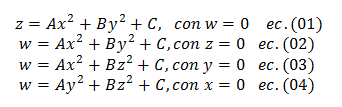
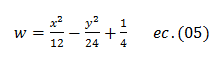
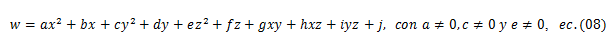
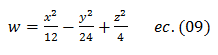
![Geometría E4D: Geometría del espacio euclidiano cuatridimensional vista desde la óptica bidimensional. (Spanish Edition) von [M., Carlos Martinez]](https://images-eu.ssl-images-amazon.com/images/I/511JZU4BaAL._SX260_.jpg)